Basic Concepts of Feedback Control
The task of maintaining these required conditions falls to one or, more usually several, process control systems with which the plant will be equipped. The practical aspects of these will be discussed more fully in the following module. The underlying principle of most process control, however, is already understood by anyone who has grasped the operation of the domestic hot water thermostat:
- The quantity whose value is to be maintained or regulated, e.g. the temperature of the water in a cistern, is measured.
- Comparison of the measured and required values provides an error, e.g.
too hot' ortoo cold’. - On the basis of the error, a control algorithm decides what to do.Such an algorithm might be:If the temperature is too high then turn the heater off. If it is too low then turn the heater on.
- The adjustment chosen by the control algorithm is applied to some adjustable variable, such as the power input to the water heater.
This summarises the basic operation of a feedback control system such as one would expect to find carrying out nearly all control operations on chemical plants, and indeed in most other circumstances where control is required. The diagram belows a feedback control loop.
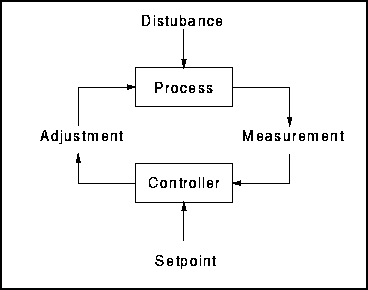
Notice that this extremely simple idea has a number of very convenient properties. The feedback control system seeks to bring the measured quantity to its required value or setpoint . The control system does not need to know why the measured value is not currently what is required, only that this is so. There are two possible causes of such a disparity:
- The system has been disturbed. This is the common situation for a chemical plant subject to all sorts of external upsets. However, the control system does not need to know what the source of the disturbance was.
- The setpoint has been changed. In the absence of external disturbance, a change in setpoint will introduce an error. The control system will act until the measured quantity reaches its new setpoint.
A control system of this sort should also handle simultaneous changes in setpoint and disturbances.
Advantages of Feedback Control
Not only does the feedback control system require no knowledge of the source or nature of disturbances, but it requires minimal detailed information about how the process itself works.
Feedback control action is entirely empirical, so long as an adjustment is being made in the correct `sense’, e.g. more heat means increasing temperature and vice versa , then the control system should remove the effect of an external disturbance.
As we will see, it helps to know more than this, but the minimum information required to make a feedback control system work is whether the adjustment makes the measurement go up or down.
Disadvantages of Feedback Control
The main disadvantage of feedback control is that the disturbance enters into the process and upsets it. It is only after the process output has moved from the setpoint that the controller takes corrective actions. Although most processes allow some fluctuation of controlled variable within a certain range, there are two process conditions which can make the overall effectiveness of feedback control quite unsatisfactory. One of these is the occurrence of disturbances of a very large magnitude. The other is the presence of a large time delay within the process.
Large Magnitude Disturbance
A very large disturbance may cause an unacceptable upset in a process before the control system can comp[enstae for it. This is most likely to occur when the relationship between the disturbance and the regulated variable is a nonlinear one in which an increasing disturbance leads to a disproportionate change in the variable.
A classic example of this is an exothermic chemical reaction whose temperature is to be regulated. Here anything that causes an increase in temperature will cause an increase in reaction rate, leading to a further increase in temperature, etc.
This is exacerbated by the extreme sensitivity of rate to temperature by the Arrhenius equation:
rate = A exp (- E/RT )
Typically a 10K rise in temperature can doubble the reaction, and hence heat production rate.
This is a situation in which feedforward control can usefully be added to a feedback control system.
Large Time Delay
It is almost always necessary to regulate the product from a process. Sometimes the only way of doing this is to adjust the feed. This puts the whole process inside the control loop, and so it may take many minutes, or even hours, for the effect of any feed adjustment to be observed in the product, see figure.
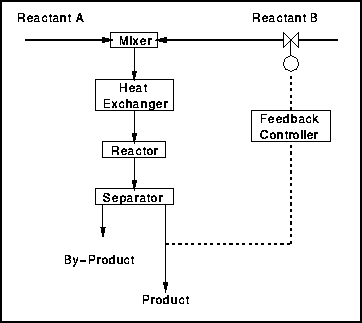
One solution is to identify some other measurable quantity which will respond more rapidly to the adjustment, and use it in a cascade control system . This is discussed later. Once again, the addition of feedforward may be helpful.