Damped Oscillation Method
Obtain a controller setting which keeps the process within acceptable limits. Use only proportional action . Note the gain setting on the controller, 
.
Disturb the process with a step change. This is most conveniently done by changing the controller setpoint. The behaviour of the process will be similar to the figure.
Damped response of process under non-optimal proportional control
The process is oscillating rather less than it would if the controller gain were 
. It is also oscillating rather more slowly, since increasing the gain of a controller speeds up the response of the process to which it is attached.
The period of oscillation, Pd , e.g. the time between successive peaks or troughs, will thus be slightly greater than Pu , but not much. Hence we can say that typically:
Pu is approximately equal to 0.95 Pd
We can estimate the increase in gain required to cause the system to oscillate continuously if we know the amount which the oscillation decays between half cycles . This would be the ratio between the amplitude of e.g. the first peak and that of the trough which follows it. This is not so easy to estimate, as the zero point of the sinusoidal respose may not be obvious. Instead take the ratios of peak-to-trough and following trough-to-peak distances. The gain would need to be increased in proportion to this ratio to cause steady oscillation.
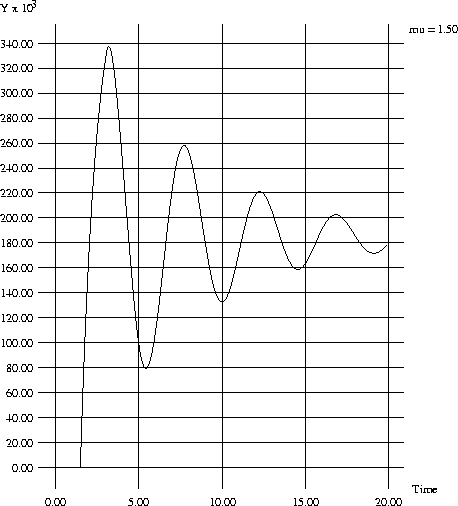
Example of Damped Oscillation Method
In the response shown above the proportional controller had a gain of 1.5.
There are 4 complete sinusoids in about 18 time units, so
Pd is approximately equal to 18/4 = 4.5
Pu = 0.95 * 4.5 = 4.28
The first peak to trough distance is about (340-80) = 260 units
The following trough to peak is (80-260) = - 180 units
The ratio of their magnitudes is thus 180/260 = 0.69
The gain should be increased by this factor, i.e:
= /0.69 = 1.5/0.69 = 2.17
Hence the ZN PI controller settings are:
Gain = /2.2 = 2.17/2.2 = 0.99
Reset = Pu / 1.2 = 4.28/1.2 = 3.57